Takes an image and applys a convolution operation to it, using a user-supplied or built-in kernel. This function uses a fast-fourier transform and does the convolution in the frequency domain, so it should be faster for much larger kernels.
render_convolution_fft(
image,
kernel = "gaussian",
kernel_dim = c(11, 11),
kernel_extent = 3,
absolute = TRUE,
pad = 50,
include_alpha = FALSE,
filename = NULL,
preview = FALSE
)Arguments
- image
3-layer RGB/4-layer RGBA array,
rayimgclass, or filename of an image.- kernel
Default
gaussian. By default, an 11x11 Gaussian kernel with a mean of0and a standard deviation of1, running from-kernel_extenttokernel_extent. If numeric, this will be the standard deviation of the normal distribution. If a matrix, it will be used directly as the convolution kernel (but resized always to be an odd number of columns and rows).- kernel_dim
Default
c(11, 11). The dimension of thegaussiankernel. Ignored if user specifies their own kernel.- kernel_extent
Default
3. Extent over which to calculate the kernel.- absolute
Default
TRUE. Whether to take the absolute value of the convolution.- pad
Default
50. Amount to pad the image to remove edge effects.- include_alpha
Default
FALSE. Whether to include the alpha channel in the convolution.- filename
Default
NULL. The filename of the image to be saved. If this is not given, the image will be plotted instead.- preview
Default
FALSE. Whether to plot the convolved image, or just to return the values.
Value
A rayimg RGBA array.
Examples
if(run_documentation()){
#Perform a convolution with the default gaussian kernel
plot_image(dragon)
}
 if(run_documentation()){
#Perform a convolution with the default gaussian kernel
render_convolution_fft(dragon, kernel=0.1, preview = TRUE)
}
if(run_documentation()){
#Perform a convolution with the default gaussian kernel
render_convolution_fft(dragon, kernel=0.1, preview = TRUE)
}
 if(run_documentation()){
#Increase the width of the kernel
render_convolution_fft(dragon, kernel = 2, kernel_dim=21,kernel_extent=6, preview = TRUE)
}
if(run_documentation()){
#Increase the width of the kernel
render_convolution_fft(dragon, kernel = 2, kernel_dim=21,kernel_extent=6, preview = TRUE)
}
 if(run_documentation()){
#Use a built-in kernel:
render_convolution_fft(dragon, kernel = generate_2d_exponential(falloff=2, dim=31, width=21),
preview = TRUE)
}
if(run_documentation()){
#Use a built-in kernel:
render_convolution_fft(dragon, kernel = generate_2d_exponential(falloff=2, dim=31, width=21),
preview = TRUE)
}
 if(run_documentation()){
#Perform edge detection
edge = matrix(c(-1,-1,-1,-1,8,-1,-1,-1,-1),3,3)
render_convolution_fft(render_bw(dragon), kernel = edge, preview = TRUE)
}
if(run_documentation()){
#Perform edge detection
edge = matrix(c(-1,-1,-1,-1,8,-1,-1,-1,-1),3,3)
render_convolution_fft(render_bw(dragon), kernel = edge, preview = TRUE)
}
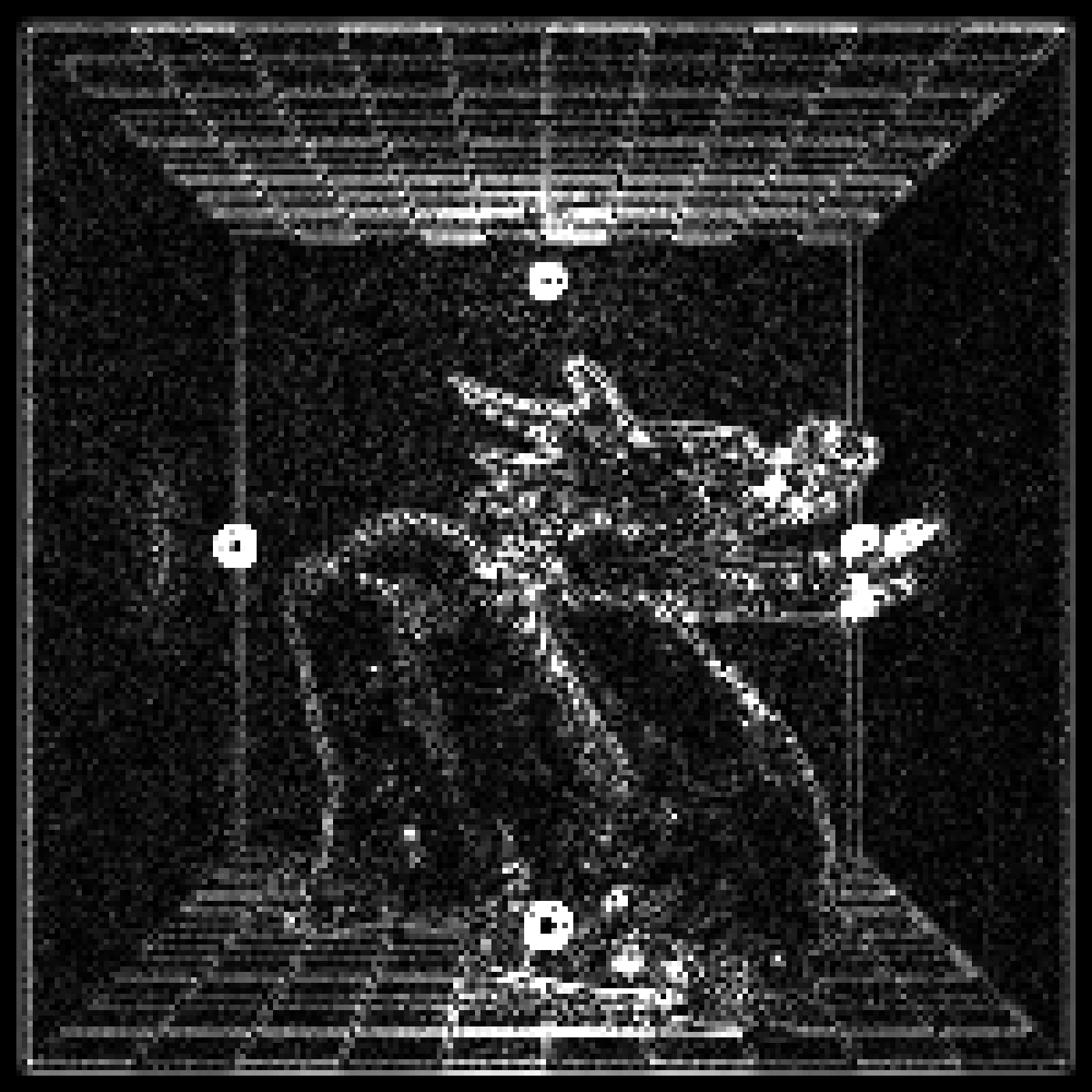 if(run_documentation()){
#Perform edge detection with Sobel matrices
sobel1 = matrix(c(1,2,1,0,0,0,-1,-2,-1),3,3)
sobel2 = matrix(c(1,2,1,0,0,0,-1,-2,-1),3,3,byrow=TRUE)
sob1 = render_convolution_fft(render_bw(dragon), kernel = sobel1)
sob2 = render_convolution_fft(render_bw(dragon), kernel = sobel2)
sob_all = sob1 + sob2
plot_image(sob1)
plot_image(sob2)
plot_image(sob_all)
}
if(run_documentation()){
#Perform edge detection with Sobel matrices
sobel1 = matrix(c(1,2,1,0,0,0,-1,-2,-1),3,3)
sobel2 = matrix(c(1,2,1,0,0,0,-1,-2,-1),3,3,byrow=TRUE)
sob1 = render_convolution_fft(render_bw(dragon), kernel = sobel1)
sob2 = render_convolution_fft(render_bw(dragon), kernel = sobel2)
sob_all = sob1 + sob2
plot_image(sob1)
plot_image(sob2)
plot_image(sob_all)
}


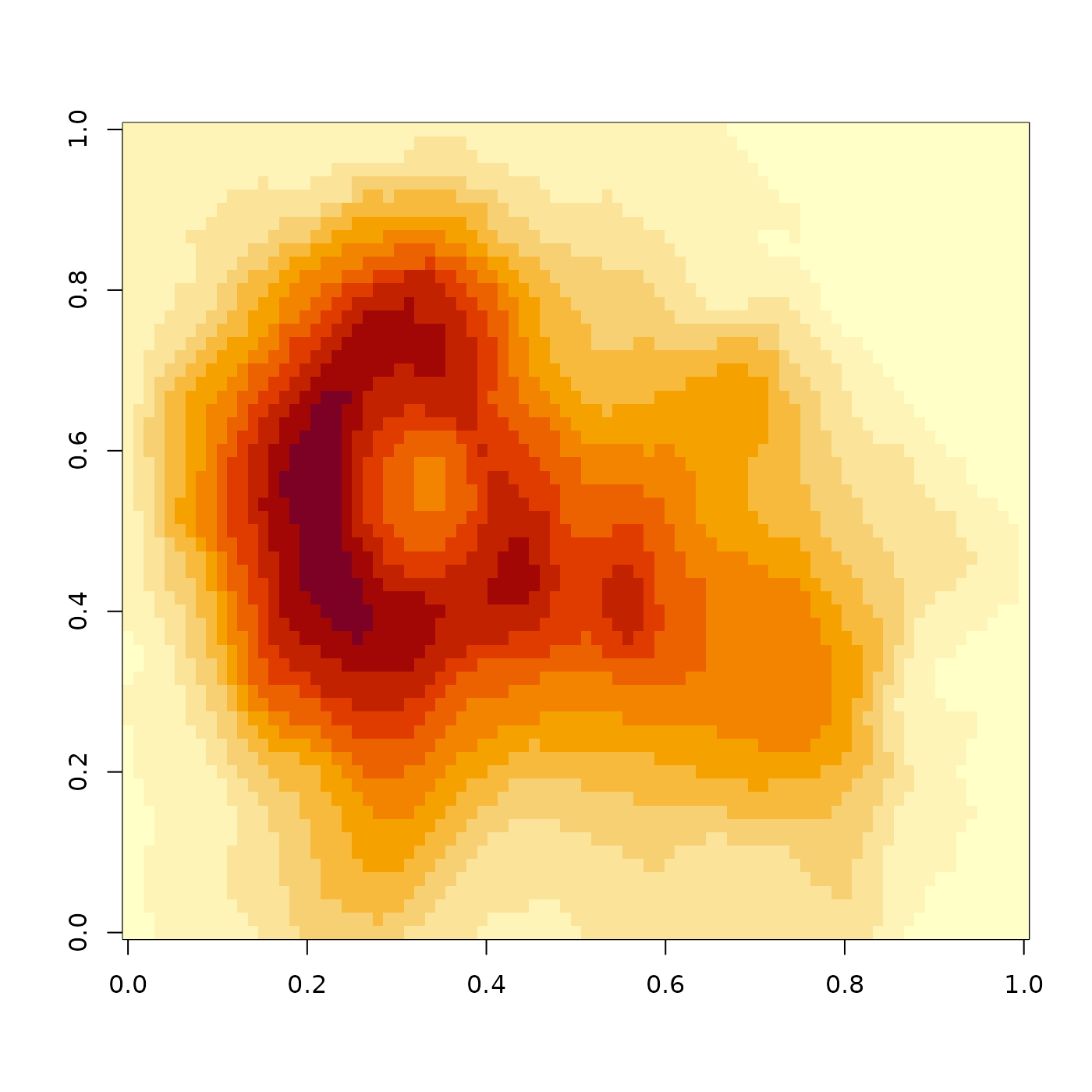
 if(run_documentation()){
#We can also apply this function to matrices:
volcano |> image()
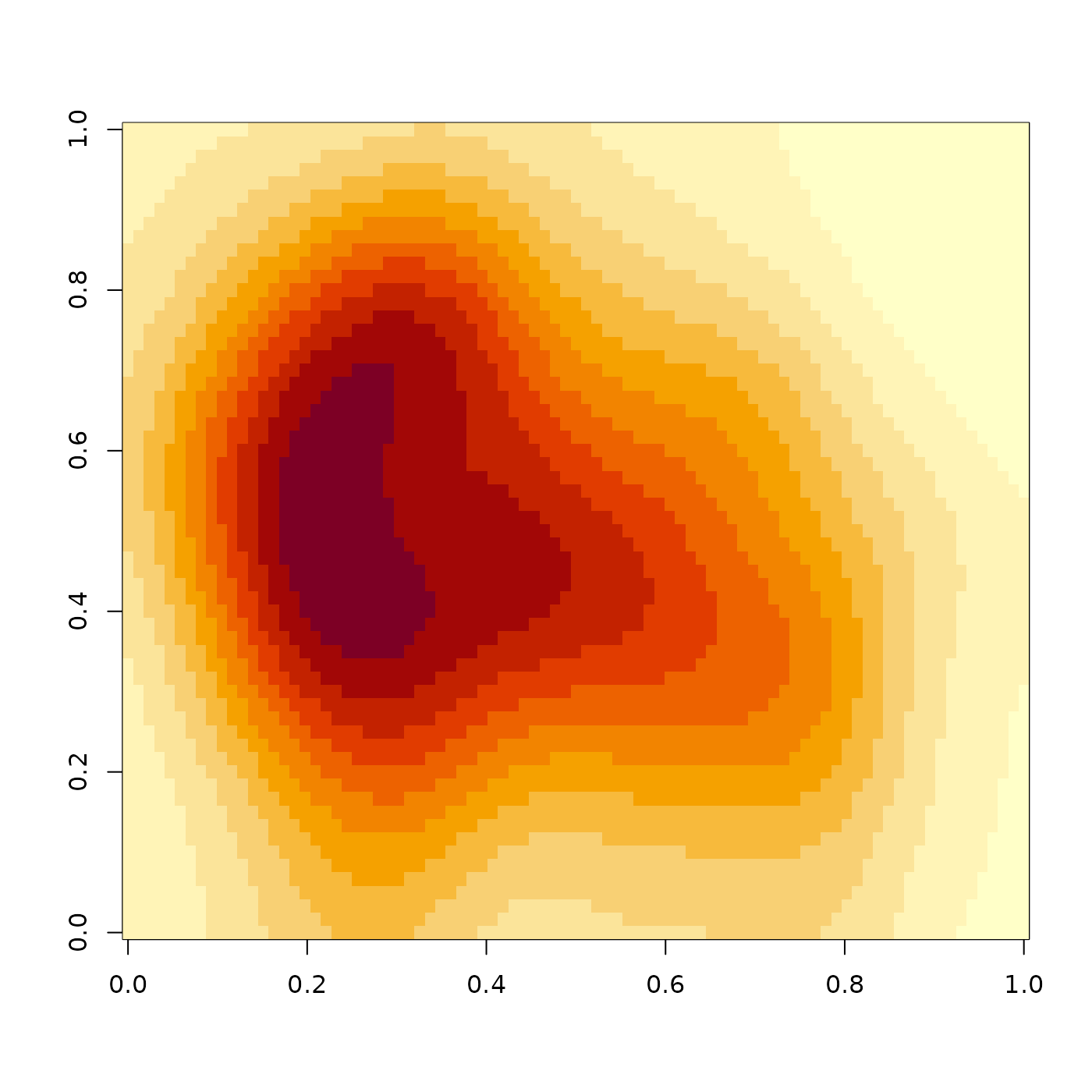
volcano |>
render_convolution_fft(kernel=generate_2d_gaussian(sd=1,dim=31)) |>
image()
}
if(run_documentation()){
#We can also apply this function to matrices:
volcano |> image()
volcano |>
render_convolution_fft(kernel=generate_2d_gaussian(sd=1,dim=31)) |>
image()
}
 if(run_documentation()){
# Because this function uses the fast-fourier transform, large kernels will be much faster
# than the same size kernels in [render_convolution()]
render_convolution_fft(dragon, kernel_dim = c(200,200) , preview = TRUE)
}
if(run_documentation()){
# Because this function uses the fast-fourier transform, large kernels will be much faster
# than the same size kernels in [render_convolution()]
render_convolution_fft(dragon, kernel_dim = c(200,200) , preview = TRUE)
}
 if(run_documentation()){
#Use a custom kernel (in this case, an X shape):
custom = diag(10) + (diag(10)[,10:1])
#Normalize
custom = custom / 20
plot_image(custom*20)
render_convolution_fft(dragon, kernel = custom, preview = TRUE)
}
if(run_documentation()){
#Use a custom kernel (in this case, an X shape):
custom = diag(10) + (diag(10)[,10:1])
#Normalize
custom = custom / 20
plot_image(custom*20)
render_convolution_fft(dragon, kernel = custom, preview = TRUE)
}

